杂物间

NWPU_算法设计(动态规划)

动态规划
基本思想:

  1. 动态规划是一种多阶段决策过程最优的通用方法.
  2. 动态规划算法与分治法类似, 其思想把求解的问题分成许多阶段或多个子问题, 然后按顺序求解各子问题. 最后一个阶段或子问题的解就是初始问题的解.
  3. 动态规划中分解得到的子问题往往不是相互独立的. 但不同子问题的数目常常只有多项式级. 用分治法求解时, 有些子问题被重复计算了许多次, 从而导致分治法求解问题时间复杂度较高
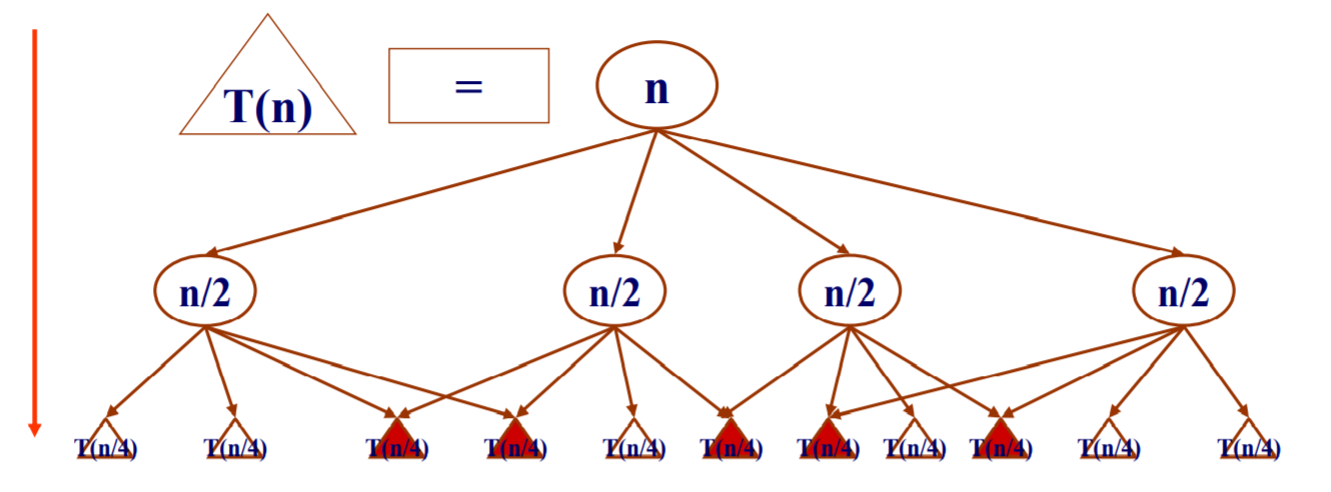
    image.png
  4. 动态规划基本思想是保留已解决的子问题的解，在需要时再查找已求得的解，就可以避免大量重复计算，进而提升算法效率.

适用条件:

  1. 求解的问题是组合优化问题.
  2. 求解的过程需要多步判断, 从小到大依次求解.
  3. 子问题目标函数最优解之间存在依赖关系(原问题最优解是由子问题最优解构成)

ex: 多起点, 多终点的最短路径
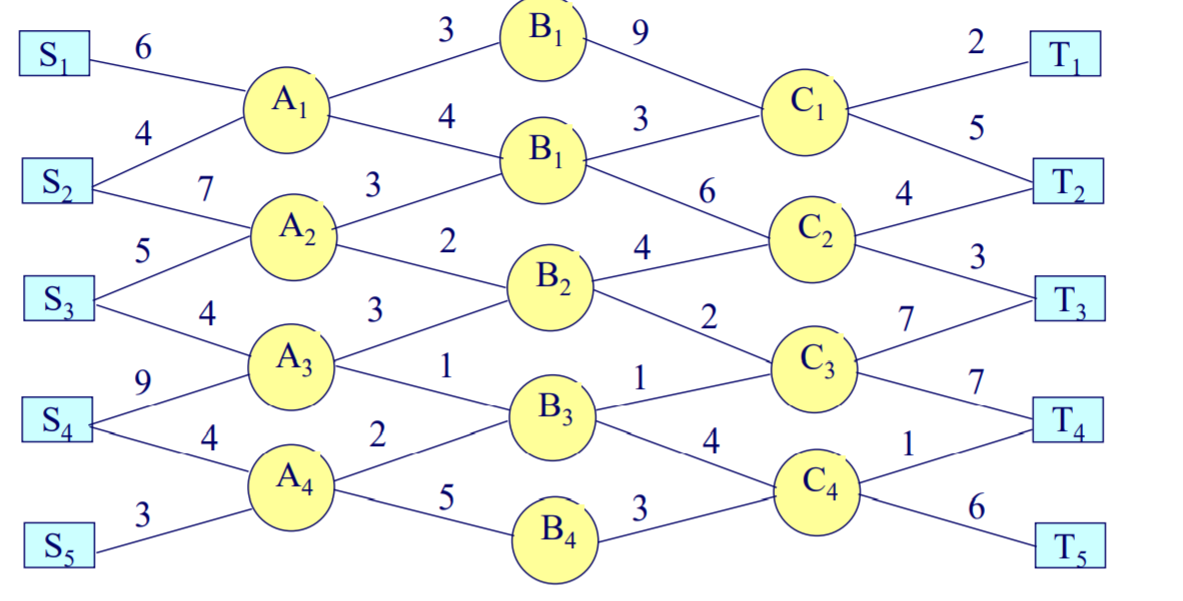
image.png

  1. 每个节点到下一层节点的最短路径之和, 即为起点->终点的最短路径
  2. 求解过程中, 需要每到一个节点判断一次最近节点信息.
  3. 以上满足动态规划条件

基本步骤:
（1）找出最优解的性质，并刻画其结构特征。
（2）递推地定义最优值。
（3）以自底向上的方式计算出最优值。
（4）根据计算最优值时得到的信息，构造最优解。
要素
最优子结构
重叠子问题
备忘录（表格）

例题1:
image.png

求解矩阵连乘问题, 首先复习一下线性代数中矩阵乘法的相关知识.
给定矩阵 a[n][m] b[m][k] 两矩阵相乘

for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                //c矩阵的第i行第j列所对应的数值，等于a矩阵的第i行分别乘以b矩阵的第j列之和
                for (int t = 0; t < k; k++)
                    c[i][j] += a[i][k] * b[k][j];

由上易得, 每当进行一次矩阵乘法, 就需要进行 nmk 次基本乘法操作.

现在回到问题中, 在矩阵连乘的情况下, 不同的乘法次序会对运算的复杂度造成影响吗?
image.png

现在可以确定, 通过优化矩阵连乘的次序, 可以大量减少运算次数.
而且我们会发现一个规律, 对于任何断开处, 总有最后一次运算是:
最前方矩阵行数 断开处矩阵列数 结尾处矩阵列数**
这一点在之后递归非常重要

我们现在需要寻找合适的"断点", 也就是从哪个位置后, 优先进行乘法运算使得最终的运算次数最少.

就如上述 A_1 A_2 A_3 三个矩阵连乘, 从A_1后断开, 先算A_2A_3, 运算次数大于从0处断开先运算A_1A_2.

我们先尝试用蛮力法求解矩阵连乘问题的最优次序情况.
蛮力法：
搜索所有可能的计算次序，并计算出每种计算次
序相应需要的数乘次数，从中找出一种数乘次数最少的计
算次序。设不同计算次序为P(n)

image.png

指数级时间复杂度, 反而影响了算法效率

我们可以重新审视一下问题
说明：
将矩阵连乘积AiAi+1…Aj简记为A[i:j]，i≤j。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵
Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全
加括号方式为(AiAi+1…AK)(Ak+1Ak+2…Aj)

计算量：
A[i:k]的计算量加上A[k+1:j]的计算量，再加上
A[i:k]和A[k+1:j]相乘的计算量。

进一步分析, 如果(AiAi+1…AK)(Ak+1Ak+2…Aj)要得到最优, 两数相乘得到最小数的情况, 即为两数都是问题范围内最小值. 满足动态规划的最优结构.
所以我们使用动态规划进行求解

1.建立递推关系
(1)设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则
原问题的最优值为m[1,n].
(2)递推方程
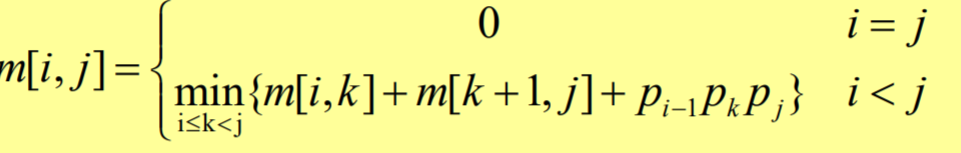
image.png
k只有j-i种可能的位置

参数说明:
p: 建立一个序列p, 存储连乘序列中矩阵的行列值. 因为前一个矩阵的列与后一个矩阵的行是同一个值, 该连乘序列才有效(才能构成矩阵乘法操作).
所以p0 = A1矩阵的行数量, p1 = A1矩阵的列数量, A2矩阵的行数量.
综上, p的维度要比连乘序列大小(矩阵个数)大 1.
s: 存储连乘序列断开的位置

递归实现

/**
     * 递归实现矩阵连乘最优位置, 寻找最少乘次
     * @param i 连乘序列的起始位置, i>0(序列从1开始)
     * @param j 连乘序列的结束位置, j<n+1(不存在第n+1个)
     * @param p 连乘矩阵序列行列值
     * @param s 存储矩阵链最少乘次
     * @return 当前矩阵链的最小乘次
     */
    int RecurMatrixChain(int i, int j, int[] p, int[][] s){

        //当传入的矩阵链长度只有1时, 最小乘次为0
        if(i == j){
            return 0;
        }
        /**
         * 初始化最小乘次值 u
         * 当从i处断开时, 将子序列 i -> i, i+1 -> j 继续进行求最小乘次处理
         * 连乘序列中p[i-1](起始位置的行数), p[k](断开位置的列数), p[j](序列末尾的列数目) 相乘
         * 上述乘积, 保存了对于当前断开点位来说所需的乘次数目
         * 对于任何断开处, 总有最后一次运算是:
         * 最前方矩阵行数* 断开处矩阵列数* 结尾处矩阵列数
         */
        int u = RecurMatrixChain(i,i,p,s) + RecurMatrixChain(i+1,j,p,s) + p[i-1]*p[i]*p[j];
        s[i][j] = i;
        for(int k = i+1; k < j; k++){
            int t = RecurMatrixChain(i, k,p,s) + RecurMatrixChain(k+1, j, p, s) + p[i-1]*p[k]*p[j];
            if(t < u){
                u = t;
                s[i][j] = k;
            }
        }
        return u;
    }

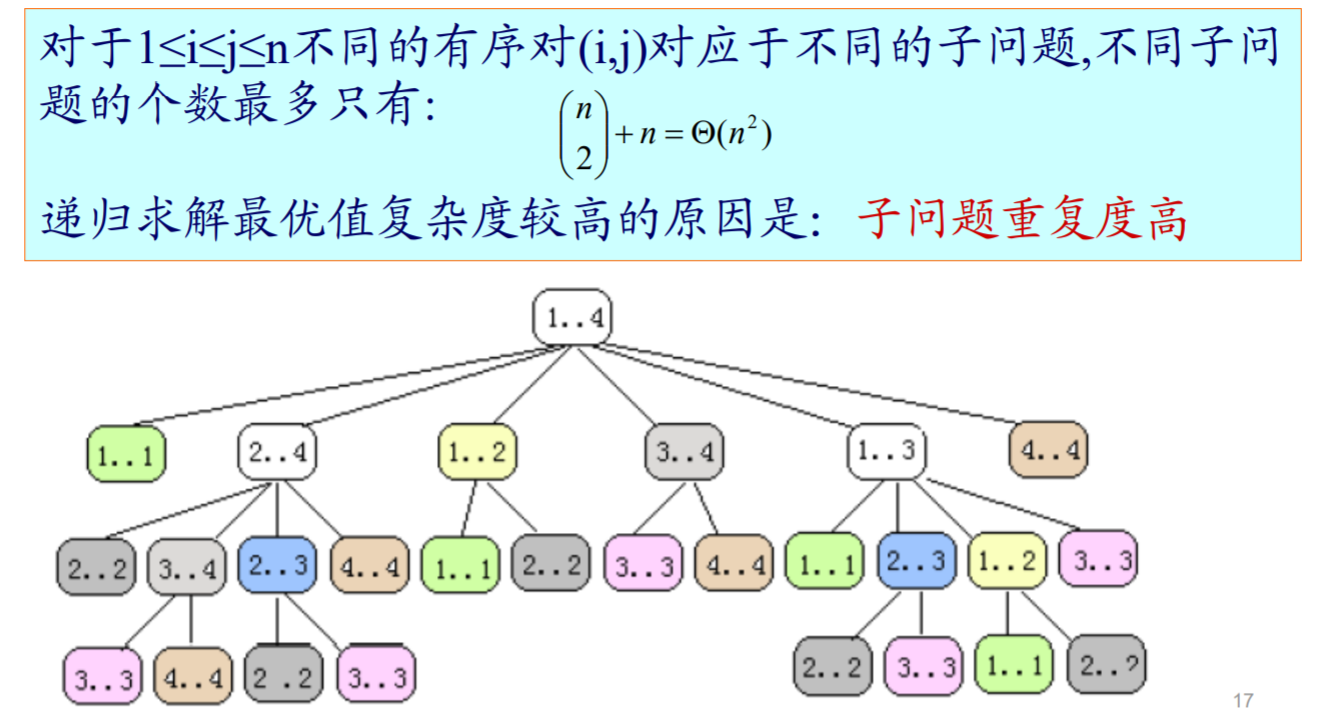
image.png

我们只需要建立一个矩阵, 保存当前矩阵链的子序列断开时, 子序列各自的最小乘次, 算到更大的序列时, 只需要调用子序列的值进行加和操作.
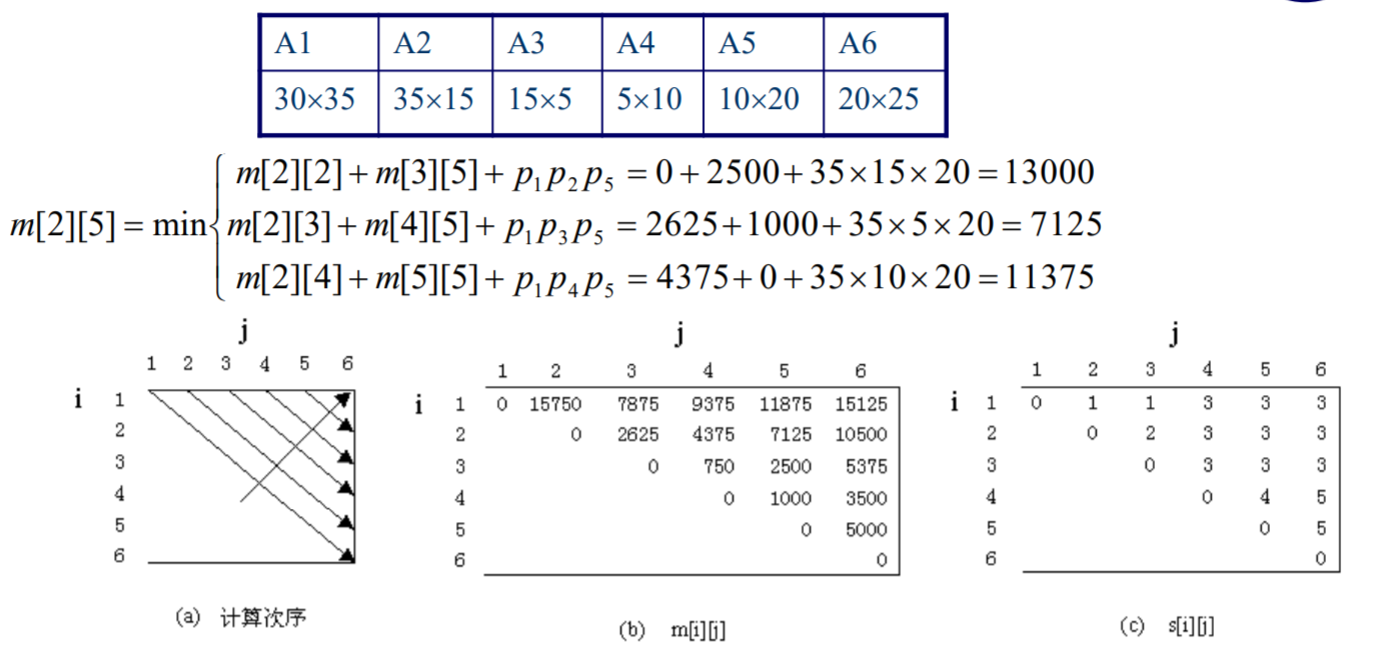
image.png

操作步骤:

  1. 从对角线开始, 向上三角依次求解. 求出的是, 针对当前断开位置
    最前方矩阵行数* 断开处矩阵列数* 结尾处矩阵列数 + 断开位置前方序列的最小乘次 + 断开位置后方的最小乘次.
  2. 保存对应位置的断开位置
/**
     * 
     * @param p 连乘矩阵行列值
     * @param n 连乘矩阵的总数目
     * @param m 连乘矩阵的最少乘次
     * @param s 连乘矩阵的断开位置
     */
    void  MatrixChain(int[] p, int n, int[][] m, int[][] s){
        
        //初始化矩阵
        for(int i = 1; i <= n; i++){
            m[i][i] = 0;
        }
        
        //进行最少乘次矩阵运算
        for(int r = 2; r <= n; r++){//从序列开始位置进行运算
            for(int i = 1; i <= n-r+1; i++){//向后依次遍历
                int j = i+r-1;
                m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
                s[i][j] = j;
                for(int k = i+1; k < j; k++){
                    int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                    if (t < m[i][j]) { //保存断开位置的最少乘次信息
                        m[i][j] = t; s[i][j] = k;
                    }
                }
            }
        }
    }

------------------------------THE END----------------------------

Hi,Friend

© 2025 杂物间